The Plaintive Sigh of a Sonic Doppelgänger: Why are Minor Chords Perceived as “Sad”? Part 3

Part 1 | Part 2 | Part 3 | Sad Song Survey

Why Minor Chords and Minor Keys are Sad: Meet the Sonic Phantoms in the Ether

To begin our investigation into the hidden cause of our peculiar perception of minor chords and keys, we will listen to a trombone quartet playing a C minor chord. We might describe the sound as "rich" or "full" or some other adjective, but what exactly is it rich with or full of? It is rich because it is full of strong partials that are created when these notes sound together. We cannot see those partials on the score, but they nonetheless exist. Modern technology allows us to hear what those harmonics sound like.



The following example is the same chord, but it has been digitally stripped of the notes that the ensemble played, so what we hear is the sound of the ethereal phantom partials by themselves, exposed by the magic of modern technology.



As stated in the example, these have not been amplified—these are the partials created by the notes played. They are part of the overall sound of the original chord. We can see the partials in a graph that shows the "spectral analysis" of the sound. For those that may be unfamiliar with a spectral analysis graph, here is how it works: The x-axis represents pitch frequency, the y-axis shows volume in decibels (dB), and spike width indicates harmonic richness (number of partials).

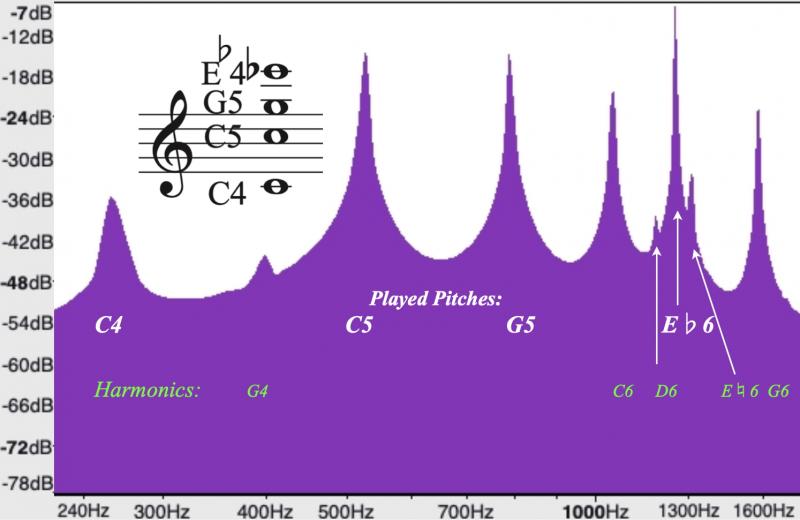
Figure 2 is a spectral analysis of the original chord. The graph illustrates the pitches present in the chord, including both the pitches actually played and the partials or harmonics created by those pitches.

Figure 2: Spectral Analysis of Trombone Quartet playing a C minor chord.>

Note that there is a C created (C4) that is of equal strength in decibels (dB) to two of the notes that were actually played (C4 and G3). There are many other harmonics that extend to 20,000Hz and beyond, beyond the range of human hearing. As can be seen from the width of the spikes, they become weaker as the frequencies increase.

Now we will compare with the sound of a flute quartet playing a C minor chord in open voicing.



Comparing the sound of the two ensembles reveals stark differences. The flute quartet is playing the same chord (in the flute's range, of course), but it does not have the powerful and striking effect of the trombone quartet. We would not likely call it "rich" or "full," and the reason is that the flutes do not produce the wide range of strong partials that the trombones do. Figure 3 is the spectral analysis of the flute quartet.

Figure 3: Spectral Analysis of Flute Quartet playing a C minor chord.

Notably, the spikes are much narrower than in the trombones, indicating that the flutes produce far fewer partials.

Here is the flute quartet with the played pitches digitally removed, which isolates the much weaker harmonics. (Note how quiet they are compared to the trombones.)



We now have our answer as to where the brass derives its power from—the nature of sound generation in trombones (vibrating lips) versus the sound generation of the flute (vibrating air column) results in strikingly different spectral profiles. This is why trombones sound like trombones and flutes sound like flutes—the partials they emphasize (or do not emphasize as the case may be) and the strength of those partials is their sonic "fingerprint." (Figure 3: Spectral Analysis of Flute Quartet playing a C minor chord.)

But why are the minor chords so much more devastating in the trombones than in the flutes? For this answer, we must focus on the pitch that creates the minor chord, namely, the E♭4. The following example removes three of the pitches played by the trombone quartet—C2, C3 and G3. The E♭4, however, remains and can be heard with the partials produced by the quartet.



It is remarkable that there is this level of dissonance present in the chord played by the trombone quartet. It is masked by the much louder pitches played by each player, but it is, nonetheless, still there.

In the following example, we hear the played E♭4 with the partials an octave up—D5, E♭5 and E♮5.



This cluster contains two minor seconds (D5-E♭5 and E♭5-E♮5), one major second (D5-E♮5), one major seventh (E♭4-D5), one octave (E♭4-E♭5) and one minor ninth (E♭4-E♮5).

Figure 4: Three Dissonant Partials sounding over E♭

This is an extraordinarily dissonant combination of pitches. If these pitches were all played together by the trombones or the flutes, it would be an Expressionist sonority that would be entirely at home in the music of Anton Webern or Pierre Boulez.

This is all presented to demonstrate that dissonances lurk in the background as the partials clash with the pitches played. The dissonances presented and heard so far contribute to the richness of the sound but are so weak that they are not heard as competing with the minor third, which, as the pitch that is actually played, easily overwhelms them.

However, there is another partial present that we have not yet encountered. In the next example, we have the original chord played by the trombone quartet with the top note, the E♭4, digitally removed. What remains is C2, C3, and G4.



Here is the spectral analysis for these pitches, comprised of only perfect intervals—a perfect octave (C2-C3), a perfect 12th (C2-G3) and a perfect fifth (C3-G3).

Figure 5: Spectral Analysis of the Trombone Quartet playing the C minor chord with the E♭ digitally removed.

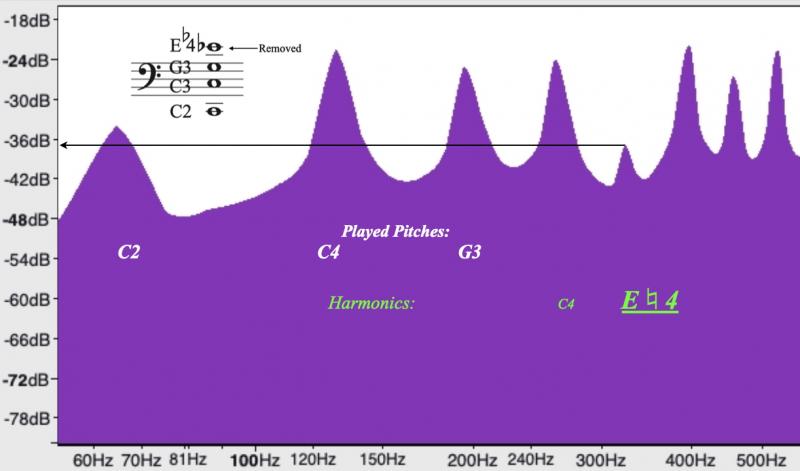
Unremarkably, E♮4 is found where expected, as the 5th partial of C2. At approximately -38 dB, it is quiet, but audible to the human ear.

Figure 6 is the original spectral analysis with the E♭4 included, we find the sounded pitch, E♭4, at -19 dB, which easily overwhelms the E♮4 and is heard as the dominant pitch.

Figure 6: Original Spectral Analysis of Trombone Quartet with the E♭included.

The frequency of E♭4 is 311.13 Hz, and E♮4 is 329.63 Hz, resulting in a "beat frequency" of 18.5 Hz.[6] For readers who may not be familiar with the term "beat frequency," a brief explanation may be helpful:

When two pitches sound, their sound waves can interfere with each other constructively and destructively, resulting in amplitude (volume) spikes when the interference is constructive and troughs when it is destructive. This produces regularly occurring "beats" as heard in the example below, where the two pitches are 1 Hz apart:



In this example, the beats occur every second. When the difference between the pitches exceeds 60Hz, we no longer hear the beat pattern; instead, we perceive the two pitches as distinct. At a beat frequency of 18.5 Hz, however, the notes are a semitone apart, and the resulting beats are occurring quickly and are heard as more of a "buzz" rather than discernible beats as found when the distance between the pitches is larger. Here is what the beat pattern sounds like for E♭4 and E♮4:



Many theorists throughout the centuries have referred to the "roughness" of the major and minor thirds. This is what we hear in the previous example which is nothing other than the quickly moving beats that buzz when E♭4 and E♮4 sound together. So, while E♮4 occurs as a partial, it is strong enough to create an audible roughness when E♭4, as a sonic interloper, is inserted into the chord. It overwhelms the naturally occurring partial, E♮4, reigning over the sonority as a usurper of the throne, like Claudius from Shakespeare's Hamlet, who murders the King to take the Danish throne, which he comes to regret before his eventual demise.

"O, my offence is rank, it smells to heaven;
It hath the primal eldest curse upon't
A brother's murder." (Hamlet, Act 3, Scene 3)

In this case, however, the E♮4 is not dead or gone; it is imprisoned within the sound and, to a large degree, hidden by the louder E♭4. We hear the E♮4 fighting with the E♭4 as a waveform with a complex relationship of 19:20. When we hear complex waveform relationships, our ear provides us with the nearest simple relationship solution.

The ear...is the one sense organ that is unerring in its sense of measurement and proportion...The ear is like a fabulous sieve, that not only sorts what it receives into large and small, but measures it exactly. It hears simple ratios as beautiful and correct sounds, and it recognizes perfectly that the purity of the octave, the fifth, or the fourth is clouded when the proportions of length or vibration frequency are not in the ratios of 1:2, 2:3, or 3:4. In the Cortian organ, it literally possesses a minute frequency meter, each tiny part of which is attuned to a certain vibration rate, and responds to a certain wavelength. When vibration combinations in the simple ratios of 1:2, 2:3, or 3:4 strike this organ, they excite particular parts of its harmoniously designed structure, which distill from the feeling of correctness the most intense pleasure. This fascinating fact of our hearing process reveals to us how closely related are number and beauty, mathematics and art. (Hindemith 23-24)

Here, Hindemith echoes the famous German physicist Hermann Helmholtz and others who also believed that we accept complex waveforms as approximations of the closest simple waveform. For example, if we encounter a complex relationship such as 2:9, then, according to this theory, we accept it as the "wrong version" of 2:8, and our brain supplies the solution. Remarkably, we can sing the note of resolution without ever having heard it.

The following example is something I have done in my classes for many years: I play a series of chords and, afterwards, ask the class to sing the "pitch that should come next." They always sing a "C." However, at no time in the example do I play a "C," so how do 25 students, who are not trained musicians, know instantly that "C" was the "right" note and adjust their vocal cords to sing that precise pitch? It is because the chords played created a complex wave pattern (for the sake of simplicity, we will call the ratio 9:8) whose nearest simple "solution" is to move the 9 (D) down to 8 (C) which is the closest simple ratio of 8:8, or 1:1. Their brains instantaneously recognized the complex waveforms, calculated the nearest simple waveform solution, and supplied them with the pitch that they wanted to hear: "C," which they pulled out of thin air.



This is the engine that gives music its power to create narratives in sound: Listeners are subconsciously calculating the waveforms' complexity and are hearing the simple solutions to those complexities. Composers capitalize on this by either providing what the listener expects to hear or surprising the listener with novel surprises, feints and misdirections. Without this, it is hard to imagine music having the power it has to capture our imagination and move us as powerfully as it does.

This remarkable and automatic human response to sound waves is perhaps stated most elegantly and succinctly by the German mathematician, Gottfried Leibniz (1646-1716), who said: "Music is a secret exercise in the arithmetic of the soul, unaware of its act of counting."

Here then, finally, is the answer to our question on why the minor chord is perceived as it is.[7] We hear the inherent dissonance that is the struggle, i.e., roughness, between the deposed E♮4 and the usurper E♭4, and we want that dissonance resolved. To put it in mathematical terms, we want the complex ratio of 19:20 made by the two pitches to move to the nearest simple relationship, which is 20:20. In other words, we recognize that the E♭4 is the "wrong" note because it is clashing with the E♮4. As the 5th partial, E♮4 is a primary and powerful member of the fundamental pitch's harmonic series that is being challenged and overrun by an extremely weak pitch that does not occur until the 19th partial, but has the strength of overwhelming force when it descends to the lower regions of the harmonic series, supplanting the 5th partial. The minor triad thus does have a naturalistic explanation linked to the harmonic series, not because it is found in the lower partials, but because the acoustical conflict from which it derives its power relies on the creation of the 5th partial. The minor third is an inversion of the harmonic series' natural hierarchy as registral power is arbitrarily given to the weak 19th partial to overwhelm the 5th partial.

Here are the two pitches played as sine waves at the decibel levels found in the previous examples.



What we hear in the previous example is the roughness previously mentioned, which is clearly audible as a fast-moving, fluttering pulsation—a dissonance arising from the complexity of the waveforms' relationship. A string length of 19 against one of 20 is irregular, which, unlike the symmetrical and simple 2:4 or 4:8, prompts our desire for resolution to a simple ratio. We know where it should resolve to, but it never does. We have therefore accepted the dissonance as one that does not need to be resolved—in doing so, we accept the minor chord and the minor key as harmonically stable. This does not, however, erase the fact that the minor chord and minor key have at their core an inherent harmonic instability and, as such, we react to the unsolved complexity with a feeling of sadness, longing (for resolution of the complex wave), melancholy and the entire host of emotions that have been conjured up by composers using the minor chord and the minor key.

The renowned German music theorist, Hugo Riemann (1849- 1919), claimed that this was not the reason for the perception of the minor triad as sad.

A certain contradiction, indeed, cannot be denied between the third of the clang ["chord" in modern parlance] and the 5th partial tone of the bass-note thus choses, which, though comparatively weak, is still audible... The 5th partial tone of the bass-note "A" is "C#," which opposes the third of the chord (C), and somewhat detracts from the physical euphony of the minor chord; but the peculiar sadness in the character of the minor chord by no means arises from the harshness of this sound, but rather from the indicated downward derivation of the notes. (Riemann 13-14)

While he did delve into the harmonic series and acoustics, Riemann was not an acoustician but rather a music theorist who was focused on developing theories regarding harmonic progressions, which he derived from surveying primary source materials, i.e., musical compositions. Riemann would not, however, have been able to isolate the harmonics as we can do today, and in doing so, arrive at a fairly precise assessment of the actual dissonance between the two pitches. Riemann, Helmholtz and others knew there was a roughness there that was audible, but none ventured further than that to claim that the dissonance was the cause of the minor triad's perceived melancholy. The fact that it is perceived as sad is incontrovertible; also incontrovertible is the fact that there must be a reason for it. The minor third in conflict, albeit muted, with the major third in the harmonic series accounts for the phenomenon very well for the following reasons:

1) First, the dissonance is not pronounced; it is veiled but subconsciously audible. We do not hear a minor chord as overtly dissonant, but we hear something that is unresolved. The dissonance between the minor third and the major third in the harmonic series easily accounts for our perception that something is wrong, or, minimally, a bit "off." If the two pitches were both played, it would be a strong dissonance that would simply sound like a wrong note in need of resolution, not a stable harmony. If the dissonance were much weaker, we would not hear it strongly enough to conflict with the major third. The major third as the 5th partial is therefore in a Goldilocks zone—not powerful enough to make it a jarring dissonance, but not weak enough to be invisible and unheard.

2) Using Allan Forte's math-oriented "set theory," we can show the major chord as a set of pitches based on the number of semitones between consecutive pitches. If the chord is C major:

· The root of the chord, C, is designated as "0";
· The third of the chord, E, is four half-steps up from C and is thus labelled "4";
· The fifth of the chord, G, is seven half-steps up and is similarly labelled numerically as "7."

As a three-note "set" in Forte's theory, it is notated as "[047]." The minor chord lowers the third by one half-step and is thus notated as "[037]." Viewing them as sets shows how the two chords flip the intervals between the root and the fifth.

Figure 7: Flipping the Thirds in a C Major and C Minor Chord

In the major chord [047], there is a major third between the root (C) and the third (E) and a minor third between the major third (E) and the fifth (G). In the minor chord [037], those are flipped and there is a minor third between the root (C) and the third (E♭) and a major third between the minor third (E♭) and the fifth (G). This inversion of the internal intervals functions, as characterized in this paper, as a doppelgänger and a trickster—the minor third is accepted as a stable interval because it so closely approximates the relationship between major third and the root/fifth by inversion. The same could not be done with the root or the fifth. Inserting a half-step from the root or fifth would destabilize the sonority and make it unusable in a tonal setting.

The minor third is thus heard as the unresolved major third that is battling with the major third that is lurking in the ethereal realm of the partials, from which our perception of sadness originates. Interestingly, in the Baroque and Classical eras, composers and performers would often resolve the minor third at the end of the piece with a major chord—this was called a "Picardy third" and was common feature in those eras, less so in later eras, although we can also find examples of it in popular music.

We are willing to accept this lack of resolution because it provides us a musical means with which to portray feelings that all human beings have as an integral part of our psychological and emotional makeup—sadness, loss, depression, melancholy, bittersweet pain, unrequited love, tragedy, anger and rage—these are all part of the human experience and need to be expressed. One cannot imagine music without the rich and meaningful expressions that are possible only because we have allowed the 19th partial, a trickster doppelgänger from high in the harmonic series, to supplant the powerful 5th partial and occupy the throne of the majestic major third.

Without this serendipitous sonic subterfuge, music would be a pale, monophonic shadow of itself, and our cultural lives would be immeasurably impoverished. As the light needs its shadow and the shadow needs its light, the major and minor similarly complement each other. In doing so, these sonorities provide us with the means to create a rich and limitless tapestry in sound, woven from our joys and sorrows, our successes and failures, as our own conflicted dualities come to life in sound.

Special thanks to:
· Dr. Bill Ryan for software assistance;
· Dr. Mark Williams and Dr. James Thompson for helping to organize the quartets;
· Sean Schafianski for help with the recording;
· The Grand Valley State University music students in the two ensembles for their kind assistance in recording the examples:
Trombone Quartet:
Matt Keith, Dylan Schoolcraft, Owen Wade, Micah Babinski;
Flute Quartet:
Julia Meyer, Hailey Briggs, Heavyn Musgrave, Brittlyn Keiler;
· and to Dr. Benjamin Whitcomb, for decades of excellent discussions on these and other topics.
Software used: Melodyne and Audacity.
Examples recorded in the Sherman Van Solkema Recital Hall at GVSU.

*"Doppelgänger No. 9," Sebastian Bieniek (B1EN1EK), 2019. Oil on canvas. 80 x 60 cm. From the "Doppelgänger" oeuvre and series. Used by kind permission of the artist.

Appendix: String Length Ratios and the Harmonic Series

These ratios refer to the position of the pitch in the harmonic series, which also coincides with the string length needed to sound each pitch. So, for the first pitch in the series, the fundamental, the string length is "1," while the second pitch in the series would sound on a string that is half the length of the fundamental. The third pitch would sound on a string that is one-third the length of the fundamental, and so on. These would be expressed as ratios 1:2 and 1:3, and the relationship between the second and third pitch would be 2:3. The simple ratios like 1:2 or 1:4 are heard as consonant because they are symmetrical. In contrast, the complex ratios are heard as dissonant because they are asymmetrical. To illustrate the symmetry, here is a picture of 1:2, 1:4, 1:8, which are four Cs—C1, C2, C3 and C4—each an octave above the previous pitch. In Figure 8, note how the nodes (points of no vibration) line up and divide the string length evenly and how ordered and pleasing the symmetry is..

Figure 8: Waveforms of C1, C2, C3 and C4

If we add the 15th partial (a B♮, or a major 7th above C4, which has a string length of 1/15 of the fundamental), it destroys the symmetry of the four perfect octaves; The nodes do not line up, and the division of the string length into 2, 4 and 8 parts is disrupted. We perceive this disruption of symmetry and we call it dissonance, which is nothing more than the interruption of symmetry that we see in Figure 9.

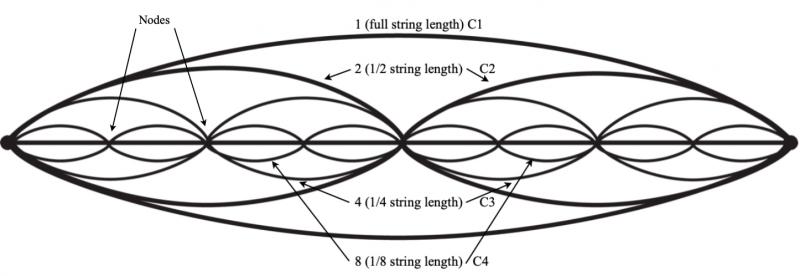
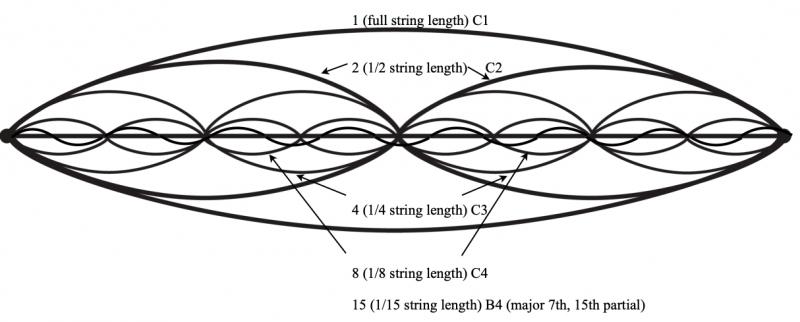
Figure 9: B4 added to the consonant four Cs in Figure 8, interfering with the symmetry.

Footnotes

[6] The simple formula for calculating beat frequency is f beat=|f 1-f 2|. For these pitches, the beat frequency is therefore 329.63 Hz -311.13 Hz = 18.5 Hz.

[7] The discussion following the quote above arrives at its conclusion as follows:

Therefore, the third must not be omitted either in the overclang or underclang; but it must also not be doubled, for then the clang obtains a striking sharpness [emphasis in original]. The doubling of the third is particularly bad when it is produced by two parts proceeding in the same direction. (Reimann 14)

Riemann is primarily concerned with which pitch should be doubled in four-part writing, and he declares that the third should not be doubled, which is what we find consistently in classical music from the common practice period (1600-1900).

Bibliography

Aristotle. De Anima. Translated by J. A. Smith, The Basic Works of Aristotle, edited by Richard McKeon, Random House, 1941, pp. 535-603.

Boethius. De Institutione Musica. Translated by Calvin M. Bower, Yale UP, 1989.

Cunningham, John G., and Randall Sterry. "Emotional Responses to Music: The Development of Musical Emotions in Childhood." Psychology of Music, vol. 26, no. 1, Apr. 1998, pp. 26-39, doi:10.1177/0305735698261004.

Dalla Bella, Simone, et al. "The Development of Music Perception in Children: Tonal Expectations and Emotion." Canadian Journal of Experimental Psychology, vol. 55, no. 2, June 2001, pp. 111-23, doi:10.1037/h0087360.

Forte, Allen. The Structure of Atonal Music. Yale University Press, 1973.

Fux, Johann Joseph. Gradus ad Parnassum. Translated by Alfred Mann, W. W. Norton, 1943.

Hauptmann, Moritz. The Nature of Harmony and Metre. Translated by W. E. Heathcote, Swan Sonnenschein, 1888.

Helmholtz, Hermann von. On the Sensations of Tone as a Physiological Basis for the Theory of Music. Translated by Alexander J. Ellis, 2nd ed., Longmans, Green, and Co., 1885.

Hindemith, Paul. The Craft of Musical Composition, Book 1. Translated by Arthur Mendel, Schott, 1942.

Huron, David. Sweet Anticipation: Music and the Psychology of Expectation. MIT Press, 2006.

Kepler, Johannes. Harmonices Mundi. Johann Planck, 1619.

Leibniz, Gottfried Wilhelm. Letter to Christian Goldbach, 17 April 1712. Die philosophischen Schriften von Gottfried Wilhelm Leibniz, edited by C. I. Gerhardt, vol. 7, Weidmann, 1890, pp. 53-54.

Lester, Joel. Compositional Theory in the Eighteenth Century. Harvard UP, 1992.

Levitin, Daniel J. This Is Your Brain on Music: The Science of a Human Obsession. Dutton, 2006.

Mersenne, Marin. Harmonie universelle. Sébastien Cramoisy, 1636-1637.

Meyer, Leonard B. Emotion and Meaning in Music. U of Chicago P, 1956.

Plato. Timaeus. Translated by Benjamin Jowett, The Collected Dialogues of Plato, edited by Edith Hamilton and Huntington Cairns, Princeton UP, 1961, pp. 1151-211.

Rameau, Jean-Philippe. Treatise on Harmony. Translated by Philip Gossett, Dover Publications, 1971.

Riemann, Hugo. Harmony Simplified, or The Theory of the Tonal Functions of Chords. Translated by H. Bewerunge, Augener, 1896.

Rossing, Thomas D. The Science of Sound. Addison-Wesley, 1982.

Rousseau, Jean-Jacques. Dictionnaire de musique. Duchesne, 1768.

Schenker, Heinrich. Harmony. Edited and translated by Elisabeth Mann Borgese, U of Chicago P, 1954.

Sorge, Georg Andreas. Vorgemach der musikalischen Composition. Georg Andreas Sorge, 1745-1747.

Sulzer, Johann Georg. Allgemeine Theorie der schönen Künste. Weidmanns Erben und Reich, 1771-1774.

Tartini, Giuseppe. Trattato di musica secondo la vera scienza dell'armonia. The Science of Music in the Age of Enlightenment, edited by Thomas Christensen, Cambridge UP, 2007, pp. 45-67.

Terhardt, Ernst. "The Concept of Musical Consonance: A Link between Music and Psychoacoustics." Music Perception, vol. 1, no. 3, Spring 1984, pp. 276-95, doi:10.2307/40285261.

Willimek, Daniela, and Bernd Willimek. "Revealing the Mystery of Emotions in Sounds: The Theory of Musical Equilibration Explains the Impact of Ordered Sounds as the Listener's Identification with Processes of Will." Auditory Perception & Cognition, vol. 6, no. 1-2, Mar. 2023, pp. 1-14, doi:10.1080/25742442.2023.2185064.

Zarlino, Gioseffo.Le istitutioni harmoniche. Source Readings in Music History, edited by Oliver Strunk and Leo Treitler, W. W. Norton, 1998, pp. 205-34.

"Why Are Minor Chords Sad and Major Chords Happy?" BBC Science Focus Magazine, 3 July 2022. Accessed 13 Apr. 2025.

Comments